Combination Tones and the Non-Linearities of the Human Ear

Last week, one of my students brought me a composition he made, which was using combination tones in an interesting compositional context, and that gave me a nudge to do some experimenting on the issue, here I’ll share what I’ve found interesting.

This is a psychoacoustic phenomenon in which, when at least two tones with close fundamental frequencies are sounded together, another tone whose frequency is the sum or difference of the original two tones is heard. This “ghost” tone is purely made up by the human ear and brain. That is, if you inspect the spectrum of the two tones with a spectrogram, this ghost tone simply isn’t there. However, this tone is usually quite faint (unless the amplitude of the original tones are high) so one needs to concentrate to get it, but it’s not very hard either.

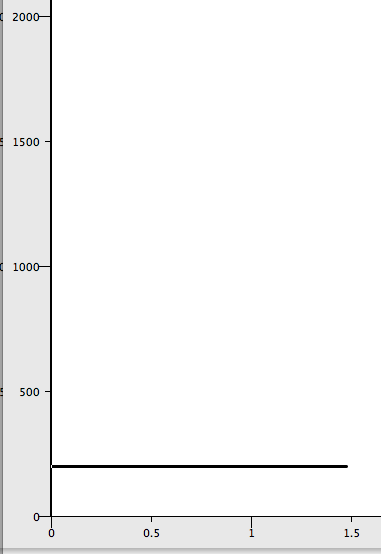
Here is an example, this is a 200 Hz sine tone:

{ SinOsc.ar(200).dup }.play

And here it is in the spectrogram:

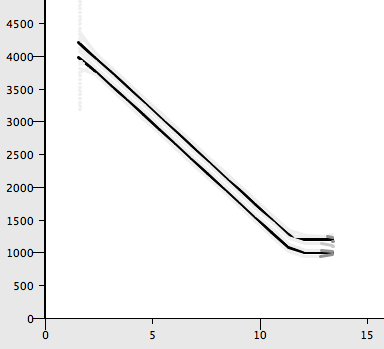
And here is 1000Hz and 1200Hz sine tones mixed together. The difference of their frequencies (200Hz) is also audible, if you pay attention (works best with headphones, but also audible with speakers. If you can’t hear it, turn the volume up):

{ SinOsc.ar([1000, 1200]).mean.dup }.play

If you can hear it, great. Here is the spectral decomposition:

Notice that there is nothing below 1000Hz here, the 200Hz tone you’ve just heard isn’t really there. As I said, this is a well known phenomenon in which the non-linearities of the inner ear causes this difference tone to be heard. Wikipedia states (although without citing a source) that, giving the two tones with different frequencies separately to each ear with headphones also create the effect but I was unable to experience this that way.

Here comes the fun part of this post, you can play several tricks with pure tones and use this ghost tone in creative ways. Here is a glissando of two pure sine tones. One oscillator starts from 4000Hz and goes down to 1000Hz, the other starts from 4200Hz and ends at 1200Hz. So the difference of their frequencies throughout is always 200Hz, so you should hear a constant (although sometimes fluctuating) 200Hz tone while the high frequencies are doing their gliss:

(
{
var freqSweep = Line.ar(4000, 1000, 10);
SinOsc.ar([freqSweep, freqSweep + 200]).mean!2;
}.play
)

Look at the spectral decomposition, and the 200Hz tone isn’t there again:

You can even go to the extremes! Here, the frequencies of the sine tones change randomly 8 times a second, but the difference of 200Hz is preserved, so you are still able to hear the constant 200Hz (not very pleasant to listen to but hey, it’s a cool effect!):

(
{
var baseFreq = TRand.ar(1000, 2000, Impulse.ar(8)).lag(0.01);
SinOsc.ar([baseFreq, baseFreq + 200]).mean!2;
}.play
)

Here they are changing 32 times a second randomly, but preserving the 200Hz separation, this is harder to hear, and fluctuates a bit, but the effect is there:

(
{//best through headphones
var baseFreq = TRand.ar(1000, 2000, Impulse.ar(32)).lag(0.01);
SinOsc.ar([baseFreq, baseFreq + 200]).mean!2;
}.play
)

And here is the grand finale of combination tones for this post. In the previous examples, we always kept a 200Hz separation between two oscillators and heard a constant difference tone. What if we craft the separation frequency in a way that the difference frequency plays a melody while the upper frequencies change randomly, even at 32 times a second? Can you hear the “bottom” melody here? Any guesses what it might be?

(
{
var times = Dseq(((1!12 ++ [1.5, 0.5, 2])!2).flat / 2, 1);
var pitchBase = [55, 55, 56, 58, 58, 56, 55, 53, 51, 51, 53, 55];
var pitches = Dseq((pitchBase ++ [55, 53, 53] ++ pitchBase ++ [53, 51, 51]).midicps, 1);
var freqs = Duty.ar(times, 0, pitches, doneAction: 2);
var baseRandFreq = TRand.ar(1000, 2000, Impulse.ar(32)).lag(0.01);
SinOsc.ar([baseRandFreq, baseRandFreq + freqs]).mean!2;
}.play;
)

Not the most beautiful thing to listen to, but try to hear the ghost melody at the bottom. Your ears and brain are playing tricks on you, and observing it is worth the suffering, in my opinion. Use the comment box if you can hear it and want to hazard a guess…